Ruixiang's blog

work harder, study better, do faster, become stronger

0%

Multi-Head & Multi-Query & Grouped-Query & Sliding-Window Attention Implementation

Posted on Edited on Views:

During current advancement of LLM, many different attention methods beyond Multi-Head Attention (MQA) from original Transformer model have been proposed, such as Multi-Query Attention (MQA) from Falcon, Grouped-Query Attention (GQA) from Llama and Sliding-Window Attention (SWA) from Mistral. Both MQA and GQA aim to save GPU memory (i.e. reduce the size of Key & Value projection matrices during attention) and speed up attention calculation (i.e. reduce size of KV cache so that read data faster and support for large batch size) without too much model performance degradation. Sliding-Window attention (SWA) is a technique used in transformer models to limit the attention span of each token to a fixed size window around it, which reduces the computational complexity and makes the model more efficient.
This blog will implement all these different attention mechanisms from scratch using PyTorch.

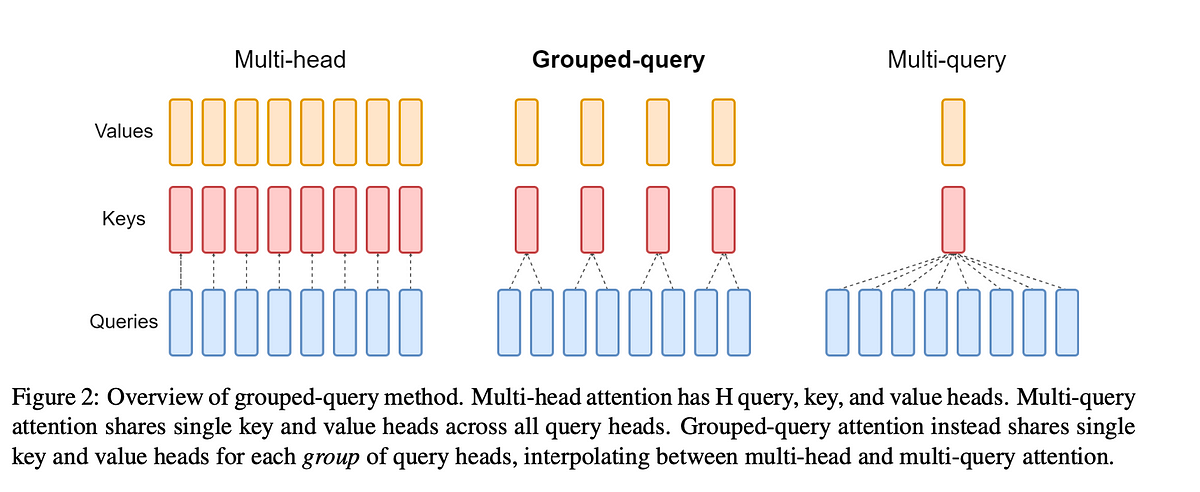
multi_query_attention

Multi-Head Attention

In Multi-Head Attention, each attention head computes its own unique set of query, key, and value vectors.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class MultiHeadAttentionScores(nn.Module):

    def __init__(self, hidden_size, num_attention_heads, attention_head_size):
        super(MultiHeadAttentionScores, self).__init__()
        self.num_attention_heads = num_attention_heads
        
        # Create a query, key, and value projection layer
        # for each attention head.
        self.query_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_attention_heads)
        ])
        
        self.key_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_attention_heads)
        ])
        
        self.value_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_attention_heads)
        ])

    def forward(self, hidden_states):
        # Create a list to store the outputs of each attention head
        all_attention_outputs = []

        for i in range(self.num_attention_heads):
            query_vectors = self.query_layers[i](hidden_states) # (batch_size, seq_len, hidden_dim)
            key_vectors = self.key_layers[i](hidden_states)
            value_vectors = self.value_layers[i](hidden_states)
            
            attention_scores = torch.matmul(query_vectors, key_vectors.transpose(-1, -2)) # (batch_size, seq_len, seq_len)
            attention_outputs = torch.matmul(attention_scores, value_vectors) # (batch_size, seq_len, hidden_dim)
            all_attention_outputs.append(attention_outputs)

        return all_attention_outputs

Multi-Query Attention

The approach of MQA is to keep the original number of heads for Q, but have only one head for K and V. This means that all the Q heads share the same set of K and V heads, hence the name Multi-Query.
In general, MQA achieves inference acceleration through the following methods:

  • The KV cache size is reduced by a factor of h(number of heads), which means that the tensors that need to be stored in the GPU memory are also reduced. The space saved can be used to increase the batch size, thereby improving efficiency.
  • The amount of data read from memory is reduced, which reduces the waiting time for computational units and improves computational utilization.
  • MQA has a relatively small KV cache that can fit into the cache (SRAM). MHA, on the other hand, has a larger KV cache that cannot be entirely stored in the cache and needs to be read from the GPU memory (DRAM), which is time-consuming.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MultiQueryAttention(nn.Module):

    def __init__(self, hidden_size, num_attention_heads, attention_head_size):
        super(MultiQueryAttention, self).__init__()
        self.num_attention_heads = num_attention_heads
        
        # Create a query layer for each attention head.
        self.query_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_attention_heads)
        ])
        
        # Create a single key layer and a single value layer
        # that will be shared by all attention heads.
        self.key_layer = nn.Linear(hidden_size, attention_head_size)
        self.value_layer = nn.Linear(hidden_size, attention_head_size)

    def forward(self, hidden_states):
        
        # Create a list to store the outputs of each attention head
        all_attention_outputs = []

        for i in range(self.num_attention_heads):
            query_vectors = self.query_layers[i](hidden_states)
            # The Key Vectors and Value Vectors computed during the forward pass are thus identical across every head.
            key_vectors = self.key_layer(hidden_states)
            value_vectors = self.value_layer(hidden_states)
            
            attention_scores = torch.matmul(query_vectors, key_vectors.transpose(-1, -2))
            attention_outputs = torch.matmul(attention_scores, value_vectors)
            all_attention_outputs.append(attention_outputs)

        return all_attention_outputs

Grouped-Query Attention

In Grouped-Query Attention, the number of unique Key and Value vectors is equal to a hyperparameter G, the number of Groups. For example, if the number of attention heads is 8 and G = 2, then there will be two unique sets of Key and Value vectors, each of which will be used by four attention heads.
GQA strikes a balance between the speed of MQA and the quality of MHA, providing a favorable trade-off.
GQA offers more efficient model parallelism across different GPUs, i.e. when operating in a multi-GPU environment with tensor parallelism, we can essentially get these performance gains for free by setting G equal to the number of GPUs.
llama2 original implementation: code In their implementation, we can see the project matrix W_k and W_v have smaller size num_kv_heads * head_dim (num_kv_heads is G) than W_q num_attention_heads * head_dim. During calculation, the code expands the Key and Value with repeat_kv(x: torch.Tensor, n_rep: int) so that Key And Value have same shape of Query: x[:, :, :, None, :].expand(bs, seq_len, n_kv_heads, n_rep, head_dim).reshape(bs, seq_len, n_kv_heads * n_rep, head_dim). Therefore, GQA doesn’t reduce the computation complexity of attention mechanism compared to MHA (Similar to MQA), it reduces the GPU memory cost of attention (i.e. Key, Value project matrices). 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class MultiHeadAttentionScores(nn.Module):

    def __init__(self, hidden_size, num_attention_heads, attention_head_size, num_kv_heads):
        super(MultiHeadAttentionScores, self).__init__()
        self.num_attention_heads = num_attention_heads
        self.num_kv_heads = num_kv_heads
        # Create a query, key, and value projection layer
        # for each attention head.
        self.query_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_attention_heads)
        ])
        
        self.key_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_kv_heads)
        ])
        
        self.value_layers = nn.ModuleList([
            nn.Linear(hidden_size, attention_head_size) 
            for _ in range(num_kv_heads)
        ])

    def forward(self, hidden_states):
        # Create a list to store the outputs of each attention head
        all_attention_outputs = []

        for i in range(self.num_attention_heads):
            query_vectors = self.query_layers[i](hidden_states) # (batch_size, seq_len, hidden_dim)
            key_vectors = self.key_layers[i % self.num_kv_heads](hidden_states)
            value_vectors = self.value_layers[i % self.num_kv_heads](hidden_states)
            
            attention_scores = torch.matmul(query_vectors, key_vectors.transpose(-1, -2)) # (batch_size, seq_len, seq_len)
            attention_outputs = torch.matmul(attention_scores, value_vectors) # (batch_size, seq_len, hidden_dim)
            all_attention_outputs.append(attention_outputs)

        return all_attention_outputs

Sliding-Window Attention

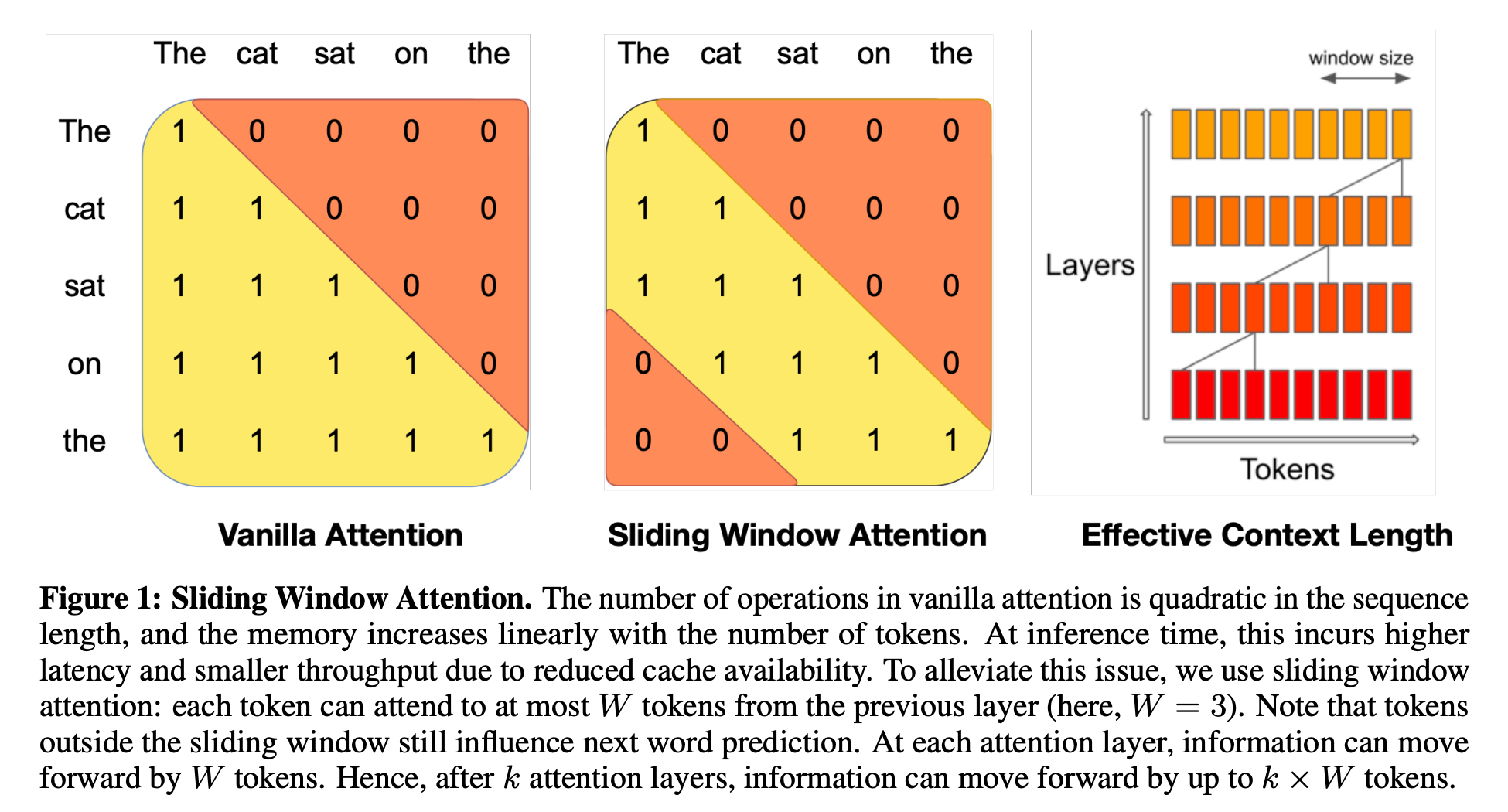
sliding_window_attn
Given the importance of local context, the sliding window attention pattern employs a fixed-size window attention surrounding each token. Using multiple stacked layers of such windowed attention results in a large receptive field, where top layers have access to all input locations and have the capacity to build representations that incorporate information across the entire input. To make this attention pattern efficient, window size w should be small compared with sequence length n. But a model with typical multiple stacked transformers will have a large receptive field. This is analogous to CNNs where stacking layers of small kernels leads to high level features that are built from a large portion of the input (receptive field). In this case, with a transformer of l layers, the receptive field size is l x w (assuming w is fixed for all layers).

Here is how Mistral implement SWA in KV cache: code

A naive PyTorch implementation of SWA:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class SlidingWindowMultiheadAttention(nn.Module):
    def __init__(self, hidden_size, num_heads, window_size):
        super().__init__()
        assert hidden_size % num_heads == 0
        self.num_heads = num_heads
        self.head_dim = hidden_size // num_heads
        self.window_size = window_size
        self.qkv_linear = nn.Linear(hidden_size, hidden_size*3)
        self.out = nn.Linear(hidden_size, hidden_size)

    def forward(self, x):
        batch_size, seq_length, hidden_size = x.size()
        padding = self.window_size // 2
        # Compute Q,K,V
        qkv = self.qkv_linear(x)
        qkv = qkv.reshape(batch_size, seq_length, self.num_heads, 3 * self.head_dim)
        qkv = qkv.permute(0, 2, 1, 3)
        queries, keys, values = qkv.chunk(3, dim=-1)
        # create sliding window for keys and values
        keys_padded = F.pad(keys, (0, 0, padding, padding), 'constant', 0)
        values_padded = F.pad(values, (0, 0, padding, padding), 'constant', 0)
        keys_windows = keys_padded.unfold(2, self.window_size, 1)
        values_window = values_padded.unfold(2, self.window_size, 1)
        # compute attention scores and context
        scores = torch.einsum('bnsd, bnsdw->bnsw', queries, keys_windows)
        attention = F.softmax(scores / (self.head_dim**0.5), dim=-1)
        context = torch.einsum('bnsw,bnsdw->bsnd', attention, values_window)
        # merge heads and combine the last two dimensions linear transformation
        context = context.reshape(batch_size, seq_length, hidden_size)
        output = self.out(context)
        return output

References

Welcome to my other publishing channels